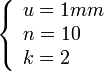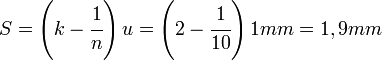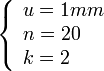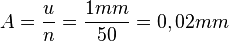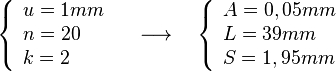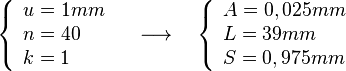MECANIZADO

PASOS PARA APRENDER A MEDIR

tratamientos termicos

extracción del hierro en alto horno



Aleaciones de fundición de hierro



PASOS BÁSICOS PARA EL USO DE LA FRESADORA



TUTORA  SOBRE FRESADORA CNC



PASOS PARA OPERAR EL TORNO

Read More

EL MICROMETRO

QUE ES UN MICRÓMETRO

El micrómetro (del griego micros, pequeño, y metros, medición), también llamado Tornillo de Palmer, es un instrumento de medición cuyo funcionamiento está basado en el tornillo micrométrico y que sirve para medir las dimensiones de un objeto con alta precisión, del orden de centésimas de milímetros (0,01 mm) y de milésimas de milímetros (0,001mm)
Para ello cuenta con 2 puntas que se aproximan entre sí mediante un tornillo de rosca fina, el cual tiene grabado en su contorno una escala. La escala puede incluir un nonio. La máxima longitud de medida del micrómetro de exteriores es de 25 mm, por lo que es necesario disponer de un micrómetro para cada campo de medidas que se quieran tomar (0-25 mm), (25-50 mm), (50-75 mm), etc.
Frecuentemente el micrómetro también incluye una manera de limitar la torsión máxima del tornillo, dado que la rosca muy fina hace difícil notar fuerzas capaces de causar deterioro de la precisión del instrumento.

 

Componentes:

Micrómetro de exteriores:

Micrómetro de interiores:

 El micrómetro usado por un largo período de tiempo, podría experimentar alguna desviación del punto cero; para corregir esto, los micrómetros traen en su estuche un patrón y una llave.

 

Historia

El primer micrómetro de tornillo fue inventado por William Gascoigne en el siglo XVII, como una mejora del calibrador vernier, y se utilizó en un telescopio para medir distancias angulares entre estrellas. En 1841, el francés Jean Laurent Palmer lo mejoró y lo adaptó para la medición de longitudes de objetos manufacturados.
El micrómetro fue introducido al mercado anglosajón en 1867 por la compañía Brown & Sharpe. En 1888 Edward Williams Morley incorporó la escala del nonio, con lo cual se mejoró la exactitud del instrumento.

Modo de Uso

I. Precauciones al medir

 Verificar la limpieza del micrómetro:

El mantenimiento adecuado del micrómetro es esencial, antes de guardarlo, no deje de limpiar las superficies del husillo, yunque, y otras partes, removiendo el sudor, polvo y manchas de aceite, después aplique aceite anticorrosivo.

No olvide limpiar perfectamente las caras de medición del husillo y el yunque, o no obtendrá mediciones exactas. Para efectuar las mediciones correctamente, es esencial que el objeto a medir se limpie perfectamente del aceite y polvo acumulados.

Utilice el micrómetro adecuadamente:

Para el manejo adecuado del micrómetro, sostenga la mitad del cuerpo en la mano izquierda, y el manguito o trinquete (también conocido como embrague) en la mano derecha, mantenga la mano fuera del borde del yunque.

II. Método correcto para sujetar el micrómetro con las manos

Algunos cuerpos de los micrómetros están provistos con aisladores de calor, si se usa un cuerpo de éstos, sosténgalo por la parte aislada, y el calor de la mano no afectará al instrumento. 

El trinquete es para asegurar que se aplica una presión de medición apropiada al objeto que se está midiendo mientras se toma la lectura.

Inmediatamente antes de que el husillo entre en contacto con el objeto, gire el trinquete suavemente, con los dedos. Cuando el husillo haya tocado el objeto de tres a cuatro vueltas ligeras al trinquete a una velocidad uniforme (el husillo puede dar 1.5 o 2 vueltas libres). Hecho esto, se ha aplicado una presión adecuada al objeto que se está midiendo.

 

Si acerca la superficie del objeto directamente girando el manguito, el husillo podría aplicar una presión excesiva de medición al objeto y será errónea la medición.

 

Cuando la medición esté completa, despegue el husillo de la superficie del objeto girando el trinquete en dirección opuesta.

Como usar el micrómetro del tipo de freno de fricción:

Antes de que el husillo encuentre el objeto que se va a medir, gire suavemente y ponga el husillo en contacto con el objeto. Después del contacto gire tres o cuatro vueltas el manguito. Hecho esto, se ha aplicado una presión de medición adecuada al objeto que se está midiendo.

III. Asegure el contacto correcto entre el micrómetro y el objeto.

Es esencial poner el micrómetro en contacto correcto con el objeto a medir. Use el micrómetro en ángulo recto (90º) con las superficies a medir.

Métodos de medición

Cuando se mide un objeto cilíndrico, es una buena práctica tomar la medición dos veces; cuando se mide por segunda vez, gire el objeto 90º.

No levante el micrómetro con el objeto sostenido entre el husillo y el yunque.

No levante un objeto con el micrómetro

No gire el manguito hasta el límite de su rotación, no gire el cuerpo mientras sostiene el manguito.

IV. Verifique que el cero esté alineado

Cuando el micrómetro se usa constantemente o de una manera inadecuada, el punto cero del micrómetro puede desalinearse. Si el instrumento sufre una caída o algún golpe fuerte, el paralelismo y la lisura del husillo y el yunque, algunas veces se desajustan y el movimiento del husillo es anormal.

Paralelismo de las superficies de medición

1) El husillo debe moverse libremente.

2) El paralelismo y la lisura de las superficies de medición en el yunque deben ser correctas.

3) El punto cero debe estar en posición (si está desalineado siga las instrucciones para corregir el punto cero).

V. Como corregir el punto cero

Método I )

Cuando la graduación cero está desalineada.

1) Fije el husillo con el seguro (deje el husillo separado del yunque)

2) Inserte la llave con que viene equipado el micrómetro en el agujero de la escala graduada.

3) Gire la escala graduada para prolongarla y corregir la desviación de la graduación.

4) Verifique la posición cero otra vez, para ver si está en su posición.

Método II )

Cuando la graduación cero está desalineada dos graduaciones o más.

1) Fije el husillo con el seguro (deje el husillo separado del yunque)

2) Inserte la llave con que viene equipado el micrómetro en el agujero del trinquete, sostenga el manguito, gírelo del trinquete, sostenga el manguito, gírelo en sentido contrario a las manecillas del reloj.

3) Empuje el manguito hacia afuera (hacia el trinquete), y se moverá libremente, relocalice el manguito a la longitud necesaria para corregir el punto cero.

4) Atornille toda la rosca del trinquete y apriételo con la llave.

5) Verifique el punto cero otra vez, y si la graduación cero está desalineada, corríjala de acuerdo al método I.

Lectura del micrómetro

¦3¦¦4¦Todos los tornillos micrométricos empleados en el sistema métrico decimal tienen una longitud de 25 mm, con un paso de rosca de 0,5 mm, de modo que girando el tambor una vuelta completa el palpador avanza o retrocede 0,5 mm.
El micrómetro tiene una escala longitudinal, línea longitudinal que sirve de fiel, que en su parte superior presenta las divisiones de milímetros enteros y en la inferior las de los medios milímetros, cuando el tambor gira deja ver estas divisiones.
En la superficie del tambor tiene grabado en toda su circunferencia 50 divisiones iguales, indicando la fracción de vuelta que ha realizado. Una división equivale a 0,01 mm.
Para realizar una lectura, nos fijamos en la escala longitudinal, sabiendo así la medida con una apreciación de 0,5 mm, el exceso sobre esta medida se ve en la escala del tambor con una precisión de 0,01 mm.
En la fotografía se ve un micrómetro donde en la parte superior de la escala longitudinal se ve la división de 5 mm, en la parte inferior de esta escala se aprecia la división del medio milímetro. En la escala del tambor la división 28 coincide con la línea central de la escala longitudinal, luego la medida realizada por el micrómetro es: 5 + 0,5 + 0,28 = 5,78.

Ver imagen:

Una variante de micrómetro un poco más sofisticado, además de las dos escalas anteriores tiene un nonio, en la fotografía, puede verse en detalle las escalas de este modelo, la escala longitudinal presenta las divisiones de los milímetros y de los medios milímetro en el lado inferior de la línea del fiel, la escala del tambor tiene 50 divisiones, y sobre la línea del fiel presenta una escala nonio de 10 divisiones numerada cada dos, la división de referencia del nonio es la línea longitudinal del fiel.
En la imagen, la tercera división del nonio coincide con una división de la escala del tambor, lo que indica que la medida excede en 3/10 de las unidades del tambor.
Esto es, en este micrómetro se aprecia: en la escala longitudinal la división de 5 mm, la subdivisión de medio milímetro, en el tambor la línea longitudinal del fiel coincide por defecto con la división 28, y en el nonio su tercera división esta alineada con una división del tambor, luego la medida es: 5 + 0,5 + 0,28 + 0,003 = 5,783
El principio de funcionamiento del micrómetro es el tornillo, que realizando un giro más o menos amplio da lugar a un pequeño avance, y las distintas escalas, una regla, un tambor y un nonio, permiten además un alto grado de apreciación, como se puede ver:

Micrómetro con nonio, indicando 5,783 mm

 

 

Tipos de micrómetros:

Características:

-  Uso: De Exteriores ; De Interiores ; De profundidad.

-  Tipo: *Mecánico; Digital ; Láser

      * o de Tambor (también suelen definirse como analógico)

-  Apreciación: Centesimales (0.01mm) ; Milesimales (0.001).

1)  Micrómetro de exteriores estándar

Mecánico:

Digital:

2)      Micrómetro de exteriores de platillos para verificar engranajes

Mecánico:

Digital:

3)      Micrómetros exteriores de puntas para la medición de roscas

4)      Micrómetro de profundidades

Caja de micrómetros de profundidad (1 micrómetro con adaptaciones).

5)      Micrómetro con reloj comparador

6)      Micrómetros de Interiores

  

Caja de micrómetro de interior con patrones:

7)      Micrómetro especial

8)      Micrómetro - pistola - de interiores digital

9)      Micrómetro de barrido láser

  

10)  Micrómetro óptico

11)  Micrómetro digital especial

 12)  Accesorios: Base de apoyo:

 Calibración de Micrómetros:
Tenemos un procedimiento para la calibración de los micrómetros de exteriores.
En dicho procedimiento no hace referencia a calibración de micrómetros de interiores o de profundidad.
Para los de interiores se deberán reemplazar los bloques patrones mencionados por anillos calibrados.
Para los de profundidad se puede utilizar el mismo procedimiento (misma cantidad de puntos y repeticiones) pero controlar con algún calibre de altura sobre un mármol. Colocamos el micrómetro de profundidad de manera que nos quede la escala hacia abajo y la parte plana hacia arriba. Ponemos el micrómetro y el calibre de altura en Cero, y luego hacemos avanzar al micrómetro y lo controlamos con el calibre. De más está decir que para que se mantenga la trazabilidad el calibre de altura deberá estar calibrado.

En los micrómetros de exterior, la calibración no es lo único necesario, además se deberá controlar las caras del micrómetro mediante lupas calibradas. Esto se realiza pra controlar la falta de paralelismo entre las caras y evitar una lectura errónea.

El procedimiento es el siguiente, se coloca el micrómetro en Cero (o en algún punto de referencia) y se lo mira mediante la lupa. Luego se lo gira un cuarto de vuelta y se vuelve a controlar. Esto se realiza hasta completar la vuelta entera, por lo tanto tendremos 4 mediciones.
Lo que se observa es que contenga las mismas cantidades de rayas en todas las mediciones.

Read More

USO DEL CALIBRADOR VERNIER

MEDICIÓN DE INTERIORES

MEDICIÓN DE EXTERIORES

MEDICIÓN DE PROFUNDIDAD

Read More

USO DEL MICROMETRO

Forma correcta de leer el micrometro

Read More

EL PIE DE REY O CALIBRADOR VERNER

Calibrador Vernier 

Un instrumento de medición es aquel elemento empleado con el propósito de contrastar magnitudes físicas distintas a través de un procedimiento de medición.
Se clasifican de acuerdo a la magnitud física que se desee medir:

Las características importantes de un instrumento de medida son:

Precisión: es la capacidad de un instrumento de dar el mismo resultado en mediciones diferentes realizadas en las mismas condiciones.

Exactitud: es la capacidad de un instrumento de medir un valor cercano al valor de la magnitud real.

Apreciación: es la medida más pequeña que es perceptible en un instrumento de medida.

Sensibilidad: es la relación de desplazamiento entre el indicador de la medida y la medida real.

Principio de funcionamiento

El sistema consiste en una regla sobre la que se ha grabado una serie de divisiones según el sistema de unidades empleado, y una corredera o carro móvil, con un fiel o punto de medida, que se mueve a lo largo de la regla.
En una escala de medida, podemos apreciar hasta su unidad de división más pequeña, siendo esta la apreciación con la que se puede dar la medición; es fácil percatarse de que entre una división y la siguiente hay más medidas, que unas veces están más próximas a la primera de ellas y otras a la siguiente.

Para poder apreciar distintos valores entre dos divisiones consecutivas, se ideó una segunda escala que se denomina nonio o vernier, grabada sobre la corredera y cuyo punto cero es el fiel de referencia. El nonio o vernier es esta segunda escala, no el instrumento de medida o el tipo de medida a realizar, tanto si es una medición lineal, angular, o de otra naturaleza, y sea cual fuere la unidad de medida. Esto es, si empleamos una regla para hacer una medida, solo podemos apreciar hasta la división más pequeña de esta regla; si además disponemos de una segunda escala, llamada nonio o vernier, podemos distinguir valores más pequeños.
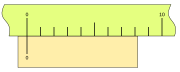
El nonio o escala vernier toma un fragmento de la regla —que en el sistema decimal es un múltiplo de diez menos uno: 9, 19, etc.— y lo divide en un número más de divisiones: 10, 20,... En la figura se toman 9 divisiones de la regla y la dividen en diez partes iguales; es el caso más sencillo, de tal modo que cada una de estas divisiones sea de 0,9 unidades de la regla. Esto hace que si la división cero del nonio coincide con la división cero de la regla, la distancia entre la primera división de la regla y la primera del nonio sea de 0,1; que entre la segunda división de la regla y la segunda del nonio haya una diferencia de 0,2; y así, sucesivamente, de forma que entre la décima división de la regla y la décima del nonio haya 1,0; es decir: la décima división del nonio coincide con la novena de la regla, según se ha dicho en la forma de construcción del nonio. Esto hace que en todos los casos en los que el punto 0 del nonio coincida con una división de la regla el punto diez del nonio también lo haga.
Cuando la división uno del nonio coincide con una división de la regla, el fiel está separado 0,1 adelante. De modo general, el fiel indica el número entero de divisiones de la regla, y el nonio indica su posición entre dos divisiones sucesivas de la regla.

Caracterización del nonio

Partiendo de una regla de divisiones igualmente espaciadas se define:

u: unidad de la regla.

Que, salvo que se especifique otro caso, toma el valor uno en la magnitud que mide la regla.
Una escala nonio se caracteriza por dos valores fundamentales:

n: número de divisiones del nonio.

k: constante de extensión.

Donde n y k son números enteros adimensionales, k mayor o igual que 1, normalmente 1 ó 2 cuando se quiere facilitar la lectura.
Y podemos ver otras características (derivadas de las anteriores):

A: apreciación, medida más pequeña que puede representar.

L: longitud del nonio, distancia entre la primera y última división del nonio, medida en la misma unidad de la regla.

S: separación entre dos divisiones sucesivas del nonio, medida en unidades de la regla.

Una escala nonio se basa en dos principios fundamentales que la definen (véase figura a la derecha):
- Una unidad de separación añadida a una unidad de apreciación deberá ser un múltiplo entero de la unidad de la regla. Este factor será la constante de extensión, es decir:

Así se establece el principio de funcionamiento explicado en la sección previa.
- El nonio desplazado n veces la medida de apreciación deberá ser igual a un desplazamiento de una unidad de la regla:

De esta forma se asegura que una y solo una división del nonio coincida con una división de la regla (exceptuando el caso donde el fiel es el coincidente).
De aquí, la apreciación es:

.

La separación entre dos divisiones del nonio se calcula:

.

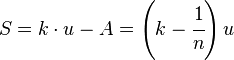Luego la longitud del nonio es:

.

Por lo tanto, tomando como unidad la división de la regla u, tenemos que la longitud del nonio L es un número entero de veces esa unidad. En la posición en la que la primera división del nonio coincida con una de la regla, la última división también coincidirá con otra división de la regla.
Se puede ver que es posible obtener la misma apreciación para distintos valores de S. A partir de un nonio que tenga una separación entre sus divisiones:

Se puede obtener otro nonio con la misma apreciación incrementando en una unidad la separación entre las divisiones de ese nonio:

Con lo que tenemos:

La separación entre las divisiones del nuevo nonio sería la que se obtendría incrementando en uno el valor de k:

Con lo que podemos obtener, para una misma apreciación A, que depende únicamente del número de divisiones n, distintas separaciones S entre divisiones del nonio y por lo tanto distintas longitudes L del nonio.
De forma general tenemos:

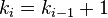
En resumen, para:

dados, y según las relaciones fundamentales, tenemos que:

Lectura del nonio

Visto lo anterior, tomando una regla graduada en milímetros, u= 1mm, veamos la lectura de un nonio con un poco más de rigor. Tomaremos como ejemplo uno de cuatro divisiones y una constante k = 2.

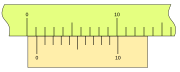
En la figura podemos ver este nonio de cuatro divisiones; la línea del fiel esta en la línea cero de la regla, y la última división del nonio coincide con la séptima de la regla.
La apreciación es un cuarto de la unidad de la regla.
Si la corredera no dispusiese de una escala nonio, no podríamos apreciar medidas inferiores a las de una división de la regla, como ya se mencionó antes. En este caso las cuatro divisiones del nonio nos permiten una apreciación de 0,25.
Podemos ver una progresión de medidas de 0,25, y la coincidencia sucesiva de las divisiones del nonio con las de la regla.
Cuando la lectura es cero (el fiel coincide con el cero de la regla) podemos ver que la última división del nonio también coincide con una división de la regla.
Al desplazarse la corredera, el fiel avanza respecto a la división cero de la regla, si la primera división del nonio coincide con una división de la regla la lectura es 0,25.
Si la corredera de desplaza más a la derecha y la segunda división de nonio coincide con una división de la regla, la lectura es 0,5.
Si la tercera división del nonio coincide con una de la regla la lectura es de 0,75.
Cuando la cuarta división del nonio coincide con una división de la regla, también lo hace el fiel, completando una unidad de la regla.
El ciclo se repite, aumentando la medida, cuando la primera división del nonio vuelve a coincidir con una división de la regla (la lectura será 1,00 1,25 1,50 ...), repitiéndose el proceso en toda la longitud de la regla.
La lectura del valor entero en la regla y la parte decimal en el nonio, con la apreciación que corresponda a su número de divisiones, da lugar a poder realizar lecturas de mediciones con mayor precisión que las unidades de la regla. Las distintas formas del nonio o vernier que se pueden construir permiten un abanico de instrumentos adaptable a las distintas necesidades, de una forma ingeniosa, económica y de gran calidad en las medidas.

Nonio de 10 divisiones

El primer ejemplo visto con anterioridad corresponde a 10 divisiones; con n = 10, tenemos que:

En el caso de que k = 2, tendríamos:

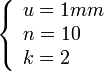
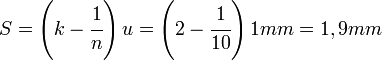
un nonio de 19 mm de longitud y 10 divisiones tendría la misma apreciación, en el doble de longitud, lo que facilitaría su lectura, al estar sus divisiones más separadas.

Otro ejemplo de nonio con n= 10 y k= 4 es el de la imagen.

Este caso de nonio en un calibre no es muy usual, siendo su característica más destacada la facilidad de lectura por la gran distancia entre sus divisiones.
En la imagen se ve un calibre con este nonio, cerrado, con lectura 0 mm.

Nonio de 20 divisiones

Podemos ver otro ejemplo, que junto con el anterior, es el más utilizado en el sistema decimal. Un nonio de 19 de longitud y 20 divisiones, con lo que tendríamos:

La longitud del nonio de 10 divisiones y k = 2 y 20 divisiones y k = 1 es la misma: 19 mm, como puede verse, pero en este segundo caso las 20 divisiones dan una apreciación de 0,05. En el caso anterior es de 0,1, por la diferencia en el número de divisiones.
Para un calibre Pie de Rey es la mayor apreciación, dado que divisiones más pequeñas no serían apreciables a simple vista, y seria necesario un equipo óptico auxiliar.
Si consideramos la posibilidad con n=20 y k=2, obtendremos una nonio de mayor longitud con la misma apreciación, así:

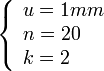
En la imagen podemos ver este caso: la apreciación del instrumento es alta, 0,05mm, pero su lectura a simple vista resulta difícil. En la imagen puede verse en 3,50 mm y difícilmente podemos determinar si la lectura es 3,45 mm ó 3,55 mm. El límite de la escala nonio viene determinado por la agudeza de la visión del usuario, que no suele superar 0,1 mm con ciertas garantías.

Nonio de 40 divisiones

Un ejemplo muy práctico y poco corriente es el nonio de 40 divisiones y una constante k= 1, con lo que tendríamos:

Este nonio tiene una apreciación de 25 micras, cada cuatro divisiones del nonio es una décima de milímetro.

Nonio de 50 divisiones

Veamos un nonio de gran apreciación, el de 50 divisiones, sobre una regla en milímetros.

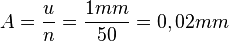
Un nonio de 50 divisiones es el de la fotografía.
La apreciación del instrumento, una división del nonio, equivale a 0,02, cada cinco divisiones son 0,02 * 5 = 0,1. En el nonio o escala vernier, se puede ver que cada cinco divisiones están marcadas con un número del 0, para indicar el fiel y comienzo de la escala, y correlativamente del 1 al 10 indicando las décimas de milímetro.
La segunda fotografía representa en detalle el nonio de la misma imagen, indicando la lectura: 3,58, con dos trazos rojos, uno indica el 3, el valor de la regla anterior al fiel, y la otra la cuarta marca después del 5 en el nonio.
Aun tratándose de una fotografía ampliada, el señalar una lectura con más precisión de 3,6 es dificultosa. Es fácil percatarse de las dificultades de este calibre para diferenciar medidas de esta precisión, y aunque sí se fabrican y comercializan calibres de esta apreciación, en la práctica, resultaría poco útil intentar realizar mediciones de más apreciación que 0,05 mm en un calibre a simple vista.

Nonios de igual longitud

La comparación de distintos nonios de igual longitud nos permite ver la importancia entre las separaciones de las divisiones, por ejemplo con u= 1mm, n=10 y k= 4, tenemos:

con una opreciación A= 0,1mm pero si tomamos los valores: u= 1mm, n=20 y k= 2, tendremos:

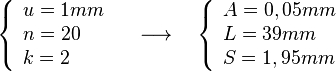
con una aprciación A= 0,05mm y con la misma longitud L= 39mm que en el caso anterior, si por el contrario tomamos: u= 1mm, n=40 y k= 1:

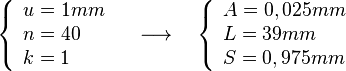
con una apreciación A= 0,025mm, viéndose cuatro divisiones para apreciar una décima de milímetro, en una misma longitud del nonio que en los casos anteriores.
Si entre dos divisiones del nonio hay más de una división de la regla, siempre cabe la posibilidad de añadir divisiones al nonio aumentando la apreciación A, y dando lugar, por supuesto, a que las distancia S de separación entre ellas sea menos.

Uso del nonio

El uso del nonio en los instrumentos de medida está muy generalizado, y se emplea en todo tipo de medidas. Es en el calibre, sin lugar a dudas, donde su utilización es más general y popular. También es utilizado en los planímetros, para cálculo de superficies.

Un mismo calibre puede ser construido con distintos nonios, según las características deseadas.

Este instrumento de medida, de gran precisión, que por su bajo coste es versátil y práctico, ha alcanzado una amplia difusión en los más distintos ámbitos.

Nonio en la escala sexagesimal

Hasta ahora hemos visto nonios o escala vernier, en el sistema decimal, donde una unidad inferior es la décima parte, esto es, un dígito a la derecha del anterior. En sistemas no decimales, como por ejemplo el sexagesimal, también se emplea este sistema de medición y la escala del nonio se puede representar en la unidad inferior.
En el sistema sexagesimal, el de medida de ángulos, por ejemplo; en grados, minutos y segundos, donde un grado son sesenta minutos y un minuto sesenta segundos, podemos emplear un nonio del siguiente modo.

Partiendo de una regla graduada en grados sexagesimal podemos ver que:

y sabemos que:

la apreciación del nonio es:

donde n es el número de divisiones, y la apreciación vendrá dada en grados sexagesimal, por tanto podemos decir:

donde la apreciación vendrá dada en minutos sexagesimal.
Buscando el número n de divisiones entre los divisores de sesenta, tendremos una escala en minutos.

Nonio angular de cuatro divisiones

Por ejemplo para n = 4 y k = 2, tenfremos:

Si hacemos k = 4, tendremos una longitud mayor, con lo que conseguimos unas divisiones más separadas, dando más claridad a la lectura y permitiendo grabar los valores de las divisiones en algunos casos:

Nonio angular de 12 divisiones

Esto es valido para distintos valores de n, procurando en toda caso, que el valor de la apreciación, resulte practica dando números redondos en la unidad que nos interesa, veamos otro ejemplo.
Si tomamos un valor de n = 12 y k = 2, nos dará:

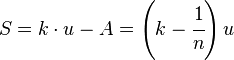Read More